
Dott. Ing. Riccardo Fecchio
riccardofecchio78![]() gmail [dot] com
gmail [dot] com
SOMMARIO
Scopo principale del presente articolo è mostrare come sia possibile calcolare le dimensioni dei crateri lunari a partire da una ripresa fotografica effettuata tramite telescopio Skywatcher Mak 127/1500 e camera di ripresa ZWO ASI 120MM Mini.
1 - Introduzione
La Luna è il nostro unico satellite naturale. Fonte di ispirazione e di riferimento per molte culture in ogni parte del mondo dall'antichità fino ai giorni nostri, ha fortemente infuenzato la vita dell’uomo, segnando in particolare l'agricoltura e la religione e dando impulso alla ricerca scientifica ma anche ispirando la poesia,
la letteratura, la fantascienza, il cinema.
La Luna, in base alla teoria attualmente più accreditata, si è formata dall’aggregazione di detriti di origine silicea derivanti dalla collisione di un grosso oggetto delle dimensioni prossime a quelle di Marte con la Terra circa 4,5 miliardi di anni fa. Anche se più piccola della Terra (circa ¼ del diametro terrestre), essa genera sul nostro pianeta un’importante influenza in quanto stabilizza l’asse di rotazione (la cui inclinazione determina il ciclo delle stagioni) ed è responsabile delle maree che si osservano in modo evidente ogni 6 ore.
Scopo principale del presente articolo è quello di mostrare come sia possibile, studiando una fotografia effettuata con telescopio, calcolare le dimensioni degli elementi della superficie lunare.
2 - Cosa è possibile osservare del nostro satellite?
Innanzi tutto è opportuno comprendere quali elementi della superficie lunare è possibile osservare dalla Terra.
La Luna mostra alla Terra (più o meno) sempre la stessa faccia perché è in rotazione sincrona con il nostro pianeta. Significa che fa un giro su se stessa esattamente nello stesso tempo che impiega a fare un giro completo intorno alla Terra (mese sidereo pari a poco meno di 27 giorni e 8 ore). Il risultato di questo moto coordinato è che l’emisfero lontano della Luna non ha mai la possibilità di trovarsi rivolto verso un osservatore terrestre. Affinché si verifichi questo fenomeno, chiamato "tidal locking", devono verificarsi due requisiti:
1. Il corpo più leggero deve orbitare lungo una traiettoria eccentrica e non circolare.
2. Il corpo più leggero non deve avere perfetta simmetria assiale: deve essere uno sferoide ed avere dunque tre momenti di inerzia differenti.
La luna rispetta entrambi i requisiti.
Guardando la Luna si notano zone più scure e zone più chiare. Osservando tali aree con i telescopi è possibile individuare, grazie al loro potere di ingrandimento, caratteristiche che ad occhio nudo sfuggono: si intravedono quindi montagne, altopiani, valli, fratture, bacini, pennacchi, crateri da impatto di asteroidi che, in assenza di atmosfera, hanno potuto raggiungere il suolo lunare senza ridurre la loro velocità, quindi la loro energia e in definitiva il loro potere distruttivo.
Gli altopiani, le zone più chiare, sono formati da calcio, alluminio, ferro e magnesio e rappresentano l’85% dell’intera superficie lunare, il 70% di quella visibile. Sono considerate le aree più antiche della Luna (4,5-4 miliardi anni). Le rocce che li costituiscono sono l'anortosite e la norite.
I mari e i bacini circolari sono zone depresse formate da lava basaltica e si presentano come macchie lisce di colore più scuro. Costituiscono il 15% dell’intera superficie lunare e rappresentano le regioni geologicamente più recenti della Luna, risalenti a 3-2,5 miliardi di anni fa.
Si riporta di seguito un'immagine generale dei mari lunari.
Figura 1 Lunar Maps – Howard L. Cohen
Per riprendere quanto osservato tramite telescopio è necessario “accoppiare” al telescopio stesso non il classico oculare ma macchine fotografiche quali le comuni reflex o camere di ripresa che usano in alcuni casi lo stesso tipo sensore CMOS oppure sensori di tipo CCD.
Figura 2 I due tipi di sensori: CCD e CMOS
Di seguito si spiegano alcuni concetti base, necessari per la comprensione del metodo adottato per il calcolo delle dimensioni degli elementi lunari fotografati.
3 - Concetti base: sensori di immagine digitali
3.1 Acquisizione dell’immagine
I sensori di immagine delle camere digitali trasformano un segnale elettromagnetico composto da fotoni, che arrivano dall’oggetto osservato con il telescopio, in un segnale elettrico proporzionale alla radiazione incidente questo fenomeno viene chiamato effetto fotoelettrico. Per fare questo i sensori sono formati da fotodiodi disposti a matrice di norma rettangolare, chiamati comunemente pixel (picture element). Opportuna circuiteria integrata traduce il segnale analogico in digitale, lo amplifica e lo memorizza, consentendo di poter successivamente ricostruirlo grazie all’utilizzo di software dedicati allo scopo.
3.2 Analisi del campo visivo fotografato
Cerchiamo di capire qual è il campo visivo inquadrato e come varia in funzione della configurazione telescopio-camera di ripresa utilizzati per riprendere un’area della volta celeste.
Si prenda a riferimento lo schema ottico qui sotto (Figura 3) che rappresenta quello del telescopio a mia disposizione, un Maksutov-Cassegrain. Da sinistra giungono i raggi dell’oggetto inquadrato, passano attraverso una lente correttrice, arrivano allo specchio primario che riflette verso il secondario (applicato sul retro della lente correttrice) che porta il fuoco dove si vede il puntino rosso e dove è posta la camera di ripresa.
Il percorso che compie la luce dal piano di ingresso al punto di fuoco si chiama lunghezza focale.
Figura 3 Schema ottico del telescopio Maksutov-Cassegrain
(Astronomical Optics - Bruce MacEvoy)
La configurazione da me adottata vede il telescopio del diametro di 127 mm con una lunghezza focale di 1500 mm e una camera di ripresa (ASI120MM) il cui sensore ha una matrice di 1280 pixel x 960 pixel da 3,75 micrometri di lato, che portano ad avere un sensore largo 4,8 mm e alto 3,6 mm.
È possibile calcolare il campo visivo, detto in gergo FOV=Field Of View), che questa configurazione dà applicando la equazione [1].
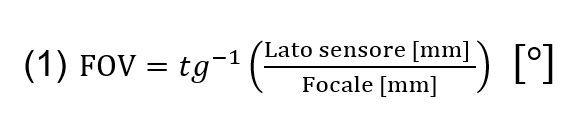
Il FOV è risultato pari a 0.18°x0.14°, circa un terzo del diametro apparente della Luna che è di circa 0.5°.
Se si vuole aumentare il FOV è necessario ridurre la focale del telescopio oppure aumentare le dimensioni del sensore.
Mantenendo fissa la camera di ripresa, e quindi il sensore, vediamo di seguito come varia il FOV in un’immagine simulata con due diverse configurazioni (si veda Figura 4):
Configurazione base del mio telescopio (riquadro rosso), → FOV 0.18° x 0.14°
Configurazione con telescopio con focale dimezzata da 750 mm (riquadro giallo) → FOV 0.37° x 0.27°
Figura 4 First Light Optics
(https://astronomy.tools)
Quello che ci mostra l’immagine sopra è che è possibile variare il FOV modificando la focale del telescopio a parità di dimensione di sensore.
C’è un altro fattore però che viene influenzato ed è la risoluzione angolare espressa in secondi d’arco per pixel [“/px]. Il simbolo “ indica il secondo d’arco che rappresenta la 3600ma parte del grado.
La risoluzione angolare rappresenta il campo inquadrato da un singolo pixel o, in termini più pratici, le dimensioni angolari più piccole che un pixel può inquadrare. La risoluzione angolare è funzione inversamente proporzionale della focale dello strumento e del numero di pixel del sensore, mentre è direttamente proporzionale alle dimensioni in mm del sensore, come si vede dalla equazione [3] riportata di seguito.
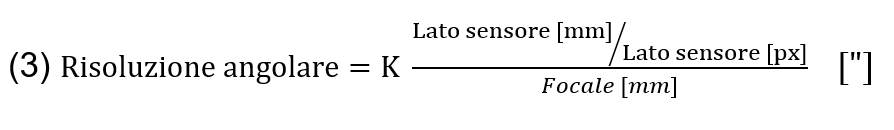
K = 206265 → fattore di conversione da radianti [rad] ad arco secondi[“]
Si nota infatti che con la configurazione 2 sebbene si possa inquadrare il doppio del FOV rispetto alla configurazione 1, a parità di grandezza di sensore, si avrà una risoluzione angolare minore, dove minore significa minore capacità di discretizzare dettagli.
Nella configurazione 1 infatti la risoluzione angolare è di 0.52"x0.52" per pixel contro i 1.03"x1.03" per pixel della configurazione 2.
Per contro, se voglio mantenere la risoluzione angolare della configurazione 1 avendo un FOV della configurazione 2, mantenendo la focale di 1500 mm, devo necessariamente avere un sensore con più pixel.
Di seguito si riporta una tabella riassuntiva degli esempi appena fatti.
Tabella 1 – Riepilogo caratteristiche delle due configurazioni analizzate
| Focale [mm] | Dim. Sensore [px] | FOV [°] | Risoluzione [“/px] |
| 1500 | 1280x960 | 0.18°x0.14° | 0.52"x0.52" |
| 750 | 1280x960 | 0.37°x0.27° | 1.03"x1.03” |
| 1500 | 2560x1900 | 0.37°x0.27° | 0.52"x0.52" |
4 - Esempio pratico: calcolo della dimensione di un cratere lunare
Una volta introdotti alcuni concetti di base, di seguito si riporta un esempio pratico di come è possibile utilizzarli per calcolare le dimensioni di un cratere conoscendo le caratteristiche di una foto.
La seguente ripresa fotografica è stata effettuata con il telescopio nella configurazione 1 ovvero con focale di 1500 mm e il sensore da 1280*960 pixel delle dimensioni di 4,8mm x 3,6mm. Con questa configurazione la risoluzione angolare è, come si è visto nei precedenti paragrafi, di 0.52"x0.52" per pixel.
Figura 5 Foto superficie lunare catturatada Fecchio Riccardo il 20/12/2020
La ripresa fotografica riportata in 5 mostra il "Mare Nectaris" della Luna, il mare principale che si vede nella metà superiore della foto. Sopra il Mare Nectaris ci sono tre crateri, più o meno delle stesse dimensioni: partendo da quello a ore 12 chiamato Theophilus, al cui interno si nota un pennacchio, si individuano successivamente, in senso antiorario, Cyrillus e Catharina. A circa ore 9 del Mare Nectaris si nota il bacino Fracastorius.
Usando il programma di grafica opensource (GIMP), o ricorrendo ad altri software similari, è possibile ricavare il diametro in pixel del cratere Theophilus. La dimensione del diametro del cratere è di circa 84 px.
Moltiplicando il diametro in pixel per la risoluzione angolare di 0.52"/px si ottiene il valore di circa 44”, ovvero l'angolo in secondi d'arco sotto cui il sensore vede il cratere, angolo che chiameremo (α).
Per conoscere il diametro del cratere in Km è sufficiente applicare la formula trigonometrica del triangolo rettangolo secondo cui la misura di un cateto è data dal prodotto dell’ipotenusa per il seno dell’angolo opposto.
Figura 6 Rappresentazione grafica dell’angolo α sotto cui viene visto un cratere di diametro D alla distanza d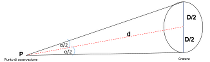
Dalla figura 6, in prima approssimazione, si ha che il cateto è metà diametro del cratere (D/2), l’ipotenusa è la distanza Terra-Luna (d) e l'angolo opposto a D/2 è la metà di quello sotto cui il sensore “vede” il cratere (α/2). Applicando quindi la formula:
![]()
Da cui D=2*393000*sen(0.00611), con α espresso in gradi e d in km.
Si ottiene quindi una misura di 83.8 Km non molto in linea con il valore ufficiale della International Astronomical Union (IAU) pari a 98.6 Km (errore del 13%).
5 - Analisi dell’errore: confronto tra teoria e pratica
L’errore ottenuto così alto è dovuto principalmente alla differenza tra i valori teorici della risoluzione angolare ricavati dalla formula (3) e quelli reali funzione della vera configurazione del treno ottico usato per la foto.
Proviamo dunque a vedere quale è effettivamente la separazione angolare facendo una sorta di taratura, ovvero una verifica pratica, empirica, sperimentale, per determinare di quanto si scosta il valore pratico da quello teorico.
Prendiamo ad esempio la foto (Figura 7) della “grande congiunzione” tra i due giganti gassosi Saturno e Giove. Non è di grande qualità è volutamente sovraesposta e modificata nei livelli del bianco e nero per evidenziare i 4 satelliti di Giove (Io, Europa, Gamimede e Callisto) e il contorno dei pianeti.
Figura 7 Foto di Saturno e Giove con i suoi 4 principali satelliti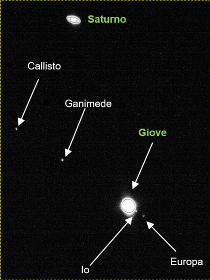
Prima di procedere oltre dobbiamo necessariamente fare una piccola premessa; quando guardiamo la volta celeste stiamo osservando gli oggetti celesti (stelle, pianeti, comete, ecc.) proiettati su di una superficie che non è piana come ci sembra, ma è sferica. Non possiamo utilizzare formule geometriche come se questi oggetti fossero disposti su un piano, dobbiamo utilizzare le formule della trigonometria sferica alle quali rimandiamo in testi specifici.
Per fortuna, per conoscere la distanza angolare tra due oggetti celesti, ci viene in aiuto il software “Stellarium”. Stellarium è un planetario gratuito Open Source che mostra un cielo in 3D proprio come si vedrebbe a occhio nudo, con un binocolo o un telescopio. Il software fornisce importanti informazioni relative agli oggetti osservati e tra le varie di funzioni tra cui la misura della separazione angolare tra due oggetti. Quindi, dati due oggetti, nel nostro caso Giove e Saturno, possiamo misurarne con “Stellarium” la loro separazione angolare utilizzando lo strumento “righello” come mostrato nella foto 8.
Figura 8 Screenshot di Stellarium con l’uso dello strumento righello per il calcolo della separazione angolare tra Giove e Saturno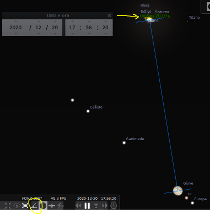
Otteniamo un valore di 9’ 20.08” che trasformati in arcosecondi danno circa 560”.
Calcoliamo ora il valore dei pixel che separano Saturno da Giove usando come strumento sempre il righello del software GIMP (vedi fig. 9). Il software ci restituisce un valore di 888.5 px.
Figura 9 Misurazione della separazione in pixel con lo strumento righello del software GIMP
Mettiamo dunque a rapporto i due valori di separazione angolare in arcosecondi trovati con Stellarium [“] e la separazione in pixel [px] trovati con GIMP e troveremo l’effettiva risoluzione angolare del nostro treno ottico [“/px].
Risoluzione angolare = 560 ” / 888.5 px = 0.630 “/px
Ecco dunque che il cratere non lo vediamo più sotto un angolo di:
| Risoluzione angolare teorica | Diametro Cratere | Angolo teorico Cratere (α) |
| 0.52 ”/px | 84 px | 44 “ |
ma di
| Risoluzione angolare teorica | Diametro Cratere | Angolo teorico Cratere (α) |
| 0.630 ”/px | 84 px | 52.94 " |
Inserendo il nuovo valore di 52.94” nella formula (4):
D=2∙393000∙sen(0.007352)=100.86 km
Otteniamo un cratere dalle dimensioni stimate di 100.86 km ovvero un valore con un errore per eccesso di appena il 2,2% rispetto ai 98.6 km ufficiali.
6 - Conclusioni
Ogni misurazione si porta dietro errori di vario tipo. La della teoria degli errori nelle misurazioni è un argomento molto vasto e trattato addirittura all’università con esami dedicati ed esula dallo scopo di questo articolo.
Nell’esempio di questo articolo abbiamo visto come l’utilizzo del valore di risoluzione angolare del treno ottico telescopio-camera di ripresa, ottenuto attraverso un calcolo teorico e non sperimentalmente, possa portare ad errori anche molto alti.
La verifica sperimentale della risoluzione angolare ha anch’essa portato ad errori, ma molto più bassi, quasi di un ordine di grandezza rispetto al calcolo teorico, poiché è stata ricavata indirettamente usando una separazione angolare nota tra due oggetti e dividendola per i pixel che li separavano nella foto.
Ad ogni modo con questo articolo ho voluto dimostrare come è possibile divertirsi, con conoscenze di scuola secondaria, con mezzi poco sofisticati e dal balcone di casa, a calcolare le dimensioni di un cratere di 100 km di diametro ad una distanza circa 4000 volte maggiore, che equivale a voler calcolare il diametro di una moneta di 1 € posta alla distanza di 90 m.
Bibliografia
[1] Howard L. Cohen “Lunar Maps For Use with the Astronomical League Lunar I Observing Program” - Revised 2012 September 20 - Published by Howard L. Cohen Gainesville, Florida
[2] Astronomical Optics - Bruce MacEvoy
[3] https://astronomy.tools
[4] International Astronomical Union (IAU) Working Group for Planetary System Nomenclature (WGPSN)